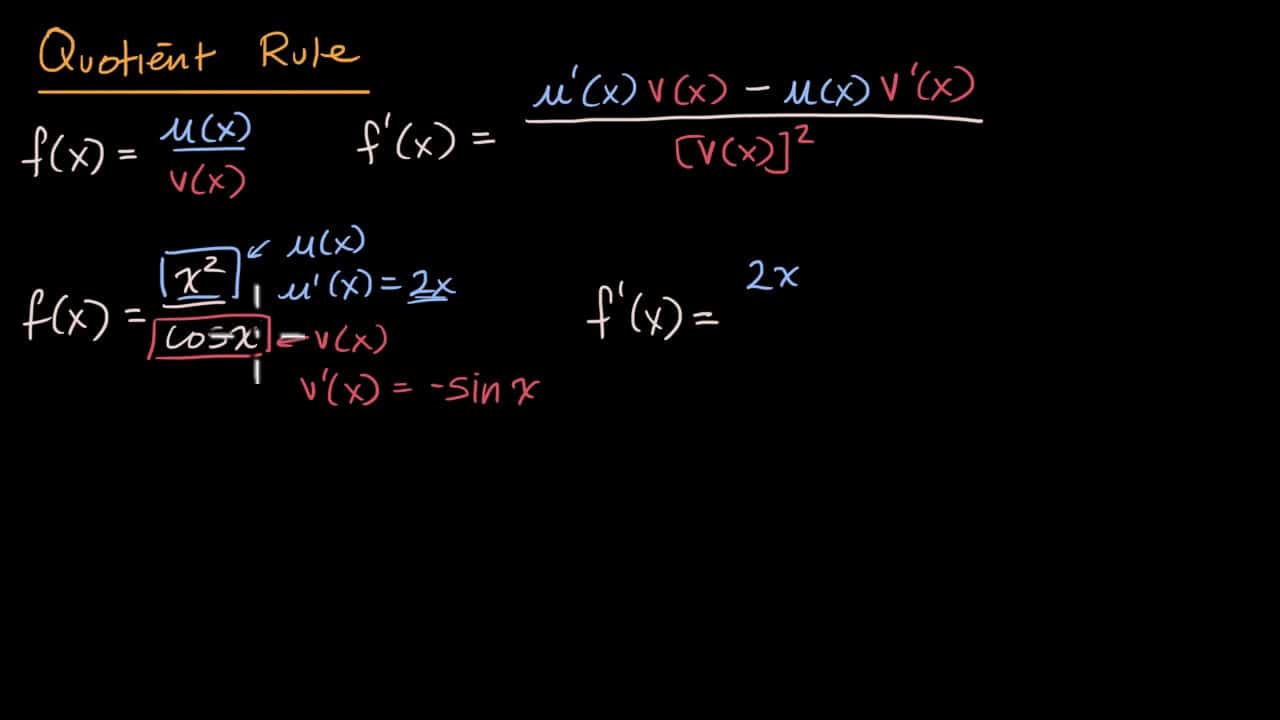بحث عن المشتقات في الرياضيات شرح كامل بالامثلة

بحث عن المشتقات في الرياضيات ، استغرق العلماء وقت طويل لتحديد تعريف المشتقات في الرياضيات . تم تسهيل الحصول على المشتقة من خلال تدوين مجموعة من القواعد سُميت بقواعد اشتقاق الدوال .

بحث عن المشتقات في الرياضيات

– هناك قواعد يمكننا اتباعها للعثور على العديد من المشتقات الرياضية . تُعرف الدالة المشتقة بأنها ميل المماس لمنحنى ق (س) عند أي نقطة و لكن مع وجود هذه المشتقة . و يكون الدليل على وجود هذه المشتقة هو إذا كانت النهاية موجودة من اليمين و اليسار عند نقطة معينة .

اقرأ ايضا

الخوارزمي مؤسس علم الرياضيات

تعريف المشتقات في الرياضيات

– إنّ معدل تغير الاقتران أو المشتقة الأولى للاقتران ق (س) عند س=س1 وفي مجاله يُرمز له بالرمز ق(س1)، كما يُستخدم الرمز ق(س1) للتعبير عن المشتقة الثانية للاقتران ق (س)، وبصورة عامة فإنّ رمز المشتقة ن للاقتران ق (س) عند س=س1 هي قن (س) حيث إنّ ن=1، 2، 3، 4، 5.

– كما يمكن تعريف المشتقات في الرياضيات أنها هي عملية توجد معدل التغير اللحظي في كمية ما . و قد استخدم العلماء المشتقات للحصول على خصائص مفيدة تتعلق بدالة مثل جذورها و نقاطها العظمى و الصغرى . إيجاد المشتقة من تعريفها شاقٌ دائمًا و لكن هناك العديد من الطرق لتخطي هذا الأمر و إيجاد المشتقات بسهولة أكبر .

– مشتق الدالة هو نسبة الفرق في قيمة الدالة f ) x) عند النقطتين x + Δx و x مع Δx ، عندما تكون Δx صغيرة جداً .
– f ‘(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

المشتق الثاني
يتم الحصول على المشتق الثاني بواسطة:

أو ببساطة استخلاص المشتق الأول:

و ” (س) = (و ‘(س))

نون مشتق
يتم احتساب مشتق nth بواسطة اشتقاق f (x) n مرات.

المشتق التاسع يساوي مشتق المشتق (n-1):

f (n) (x) = [f (n-1) (x)] “

مثال:
أوجد المشتق الرابع لـ f (x) = 2×5

و (4) (س) = [2 × 5] “” = [10×4] “” = = [40 × 3] “= [120 × 2] ‘= 240 ×

قواعد المشتقات في الرياضيات

– من أهم قواعد الأإشتقاق على الإطلاق هى قاعدة chain rule
المفهوم البسيط منها يقتضى انه اذا كانت ص = [د(س)]^ن : فإن : صَ = ن [د(س)]^(ن-1) × دَ(س)

القاعدة الثابتة

– هذا بسيط. f (x) = 5 عبارة عن خط أفقي له ميل يساوي صفرًا ، وبالتالي مشتقته هو أيضًا صفر.

قاعدة الاقتران كثير الحدود

– إذا كان ق (س)=سن، حيث إنّ ن تنتمي مجموعة الأعداد الطبيعية بدون العدد صفر، فإنّ ق (س)=ن س(ن-1).

قاعدة الجمع والطرح

– إذا كان ق (س)، هـ (س) اقتراناً قابلاً للاشتقاق عند س، وكانت جـ تنتمي مجموعة الأعداد الحقيقية فإنّ : ك (س)=جـ×ق (س) قابل للاشتقاق عند س، ويكون ك (س)=جـ×ق (س) .

– ع (س)=ق (س)+هـ (س) قابل للاشتقاق عند س، ويكون ع (س)=ق (س)+هـ (س) .
– ل (س)=ق (س)-هـ (س) قابل للاشتقاق عند س، ويكون ل (س)=ق (س)-هـ (س).

قاعدة الضرب 

– مشتقة حاصل ضرب اقترانين : إذا كان كلّ من ق (س)، هـ (س) اقترانين قابلين للاشتقاق عند س، وكان ع (س)=ق (س)×هـ (س) فإنّ: الاقتران ع (س) قابل للاشتقاق عند س، ويكون ع (س)=ق (س)×هـ (س)+ق (س)×هـ (س).

قاعدة القسمة 

– مشتقة ناتج قسمة اقترانين: إذا كان كل من ق (س)، ع (س) قابلاً للاشتقاق عند س، ع (س) لا يساوي صفر ، فإنّ: غ (س)=ق (س)/ع (س) قابل للاشتقاق عند س، ويكون غ (س)=[ق (س)×ع (س)]-[ع (س)×ق (س)]/(ع (س))2.

قاعدة القوى الكسرية

– إذا كانت ص=س م/ن، حيث إنّ (م/ن) عدد نسبي فإن دص/دس=(م/ن) س(م/ن) -1.

أمثلة على المشتقات في الرياضيات

المثال الأول

f (x) = x3 + 5×2 + x + 8

f ‘(x) = 3×2 + 2⋅5x + 1 + 0 = 3×2 + 10x + 1

المثال الثاني

(و (خ) = خطيئة (3 × 2)

المثال الثالث

f ‘(x) = cos (3×2) ⋅ [3×2]’ = cos (3×2) ⋅ 6x

المثال الرابع

f ‘(x0) = 0

أمثلة متنوعة على المشتقات في الرياضيات

– د(س) = س² + 1

دَ(س) = 2س

حيث ان مشتقة الثابت = 0

مثال 2) د(س) = س³ + 2س + 4

دَ(س) = 3س² + 2

تم تطبيق اعدة chain rule ، وعرفنا ان مشتقة 4 = 0

مثال 3) د(س) = س³ س²

دَ(س) = 3س² س² + 2س س³

تم تطبيق قاعدة الضرب product rule

نرتب ما سبق : دَ(س) = 3س^4 + 2س^4
= 5 س^4

س^4 + 3
مثال 4) د(س) = ــــــــــــــــــــــــــ
س + 1

4س³ – (س^4 + 3)
دَ(س) = ــــــــــــــــــــــــــــــــــــ
(س+1)²

ملاحظة : رمز المشتقة الأولى يرمز له كـ َ مثلاً دَ(س)
وكذلك نعبر عنه بـ

س ديس

والمقصود منها معدل تغير ص / معدل تغير س النهـايات ..

أسئلة عن المشتقات في الرياضيات

بحث عن المشتقات في الرياضيات

اوجد معدل التغير للدالة د بحيث
د(س) = جذر(س+3) عند س=1
ومن ثم اوجد قياس الزاوية التى
يصنعها المماس لمنحنى الدالة
د عند :
-11
س = ــــــــــ
4

فى الإتجاه الموجب لمحور السينات … الحلـــــــــ

د(س) = جذر(س+3)  بالتحويل الى الصورة الاسية

د(س) = (س+3)^½ بتطبيق قاعدة chain rule

Let (s) = 0 (c + 3) ^ – 2

دع (1) = ½ (1 + 3) ^ – ½ = ½ (4) ^ – ½

1
= ½ × جذر(4)^-1 = ½ × جذر(ـــــــ)
4

= ½ × ½ = ¼

المطلوب الثانى لكى نوجد الزاوية التى يصنعها المماس
نعوض ايضاً فى المشتقة، ثم نوجد الميل بطريقة
ظاهـ = الميل  حيث هـ الزاوية المحصور بين معادلة المماس
ومحور السينات فى الإتجاه الموجب له ..

1111 َ11
َ (ـــــــــــ) = ½ (ــــــــــ + 3) ^ – ½
4 4

بتوحيد المقامات داخل القوس، كالتالى
( سأذكر هذه الخطوة اولاً ..)
ما داخل القوس هو :

– 11           3       (1×-11) + (3×4)
ـــــــــــــ + ــــــــــ = ـــــــــــــــــــــــــــ
4             1              4 × 1

1
= ــــــــــ
4

لاحظ كل هذه الخطوات تتم ذهنيا، وضعتها
من اجل التوضيح فقط، ولا داعى لكتابتها
فى ورقة الإمتحان .. عرفنا ان ما داخل
القوس = ¼ بالتعويض

المشتقة = ½(¼)^-½

= ½ جذر(¼)^-1 = ½جذر(4)

= ½ × 2 = 1

وهنا ملحوظة هامة جداً جذر(¼)^-1
لكى نلغى الأس السالب نقلب الكسر فقط ..

الآن الميل عندما س = -11 / 4  هو 1

الميل = ظاهـ = 1

ما هى الزاوية التى ظلها = 1 ؟؟
على الآلة اضغط shift tan (1) =         ll
بنظام الرديان الزاوية = ط/4
بالنظام الستينى الزاوية = 45 ْ

وبهذا انهينا بحمد الله بحث عن المشتقات في الرياضيات